Multi-Objective Decision Optimization in PLEXOS® Integrated Energy Models

Introduction

As digital data technologies become more advanced every day and more competition arises within the Energy industry and all other sectors, it becomes clear that optimizing data-based decisions is critical to competing in the market. Big data gives businesses access to more information not so easily accessible in the past, nor was it ever at today’s scale. However, to stay competitive, optimizing data-based decisions is pivotal to running a successful business now as the nature of competition changes. In this White Paper, I introduce MultiObjective Decision Optimization within PLEXOS and how technological advances allow for increased decision-making capability despite complex market dynamics and an increased rate of change.

The capacity available in PLEXOS 8.3 and the latest versions for conducting Multi-Objective Decision Optimization studies is fully available to the integrated Energy modeling communities of Power, Gas, Water, and renewable energy markets’ users to make the most informed decisions at the most impactful times.

Complex Global Challenges and Tectonic Changes

During the last decade, strong and sometimes violent transitions and tectonic changes have occurred. Global politics are in turmoil, with multiple significant geopolitical competitions extending and unavoidably affecting global energy markets. The global energy market is in flux due to the recent security of energy supply issues in Europe and strong cross-competitions between different energy sources stemming from the need to address climate change through green measures and initiatives. Complexity arises from the adoption of new clean and sustainable energy technologies, while parallel tectonic shifts are taking place in science and in technologies, particularly in digital transformations.

The Opportunity of Gaining a Greater Insight into Complexity

With so many new variables and vastly different time horizons in the energy investment landscape, the cost of wrong decisions may be much higher and more challenging from which to recover. From a scientific perspective, optimizing Energy Investments and Operations becomes a complex mathematical problem. Advanced Digital information technology and computing methods are required to solve problems, and they are the only tools and methods to effectively support decision-making and address the increased uncertainty and complexity of this new era. Furthermore, most—if not all —modern Energy sector and related (e.g., Environmental) problems fall within the definition of Multi-Criteria Decision-Making under Uncertainty and Risk.

The ability to address all the different potential futures and objectives and what might happen in the energy markets is more critical than ever to be able to meet the decision-making needs of the various shareholders that are active in the energy & related sectors. The more successful our industry can be in addressing these potential futures, enabling such a seamless multi-objective decision optimization support as In PLEXOS, the greater the chances we have to achieve sustainable growth and enhanced future prosperity and quality of life.

Analytics and Decision Optimization

When it comes to Decision Optimization, Prescriptive analytics represents the only set of analytical methods available that directly supports final decision-making (what I can best do?) with actions that need to be taken.

"…If you are in a competitive marketplace—managing anything from products to people—prescriptive analytics could mean a huge boost to profit, productivity, and the bottom line. And honestly: it’s still early in the prescriptive analytics game. I’m guessing we’re only seeing the tip of the iceberg in terms of what prescriptive analytics can accomplish."

Daniel Newman (Contributor) - Why The Future Of Data Analytics Is Prescriptive Analytics, FORBES, Jan 2, 2020. ¹

Prescriptive analytics is the highest capability of analytics today that decides in improving the firms through the predictive and descriptive analytics. ²

Multi-Objective Optimization v Single-Objective Optimization

The University of Wisconsin-Madison, US presents an optimization taxonomy to in which⁵, Multi-Objective Optimization in highly ranked. It stands next to the Deterministic and Uncertainty methods.

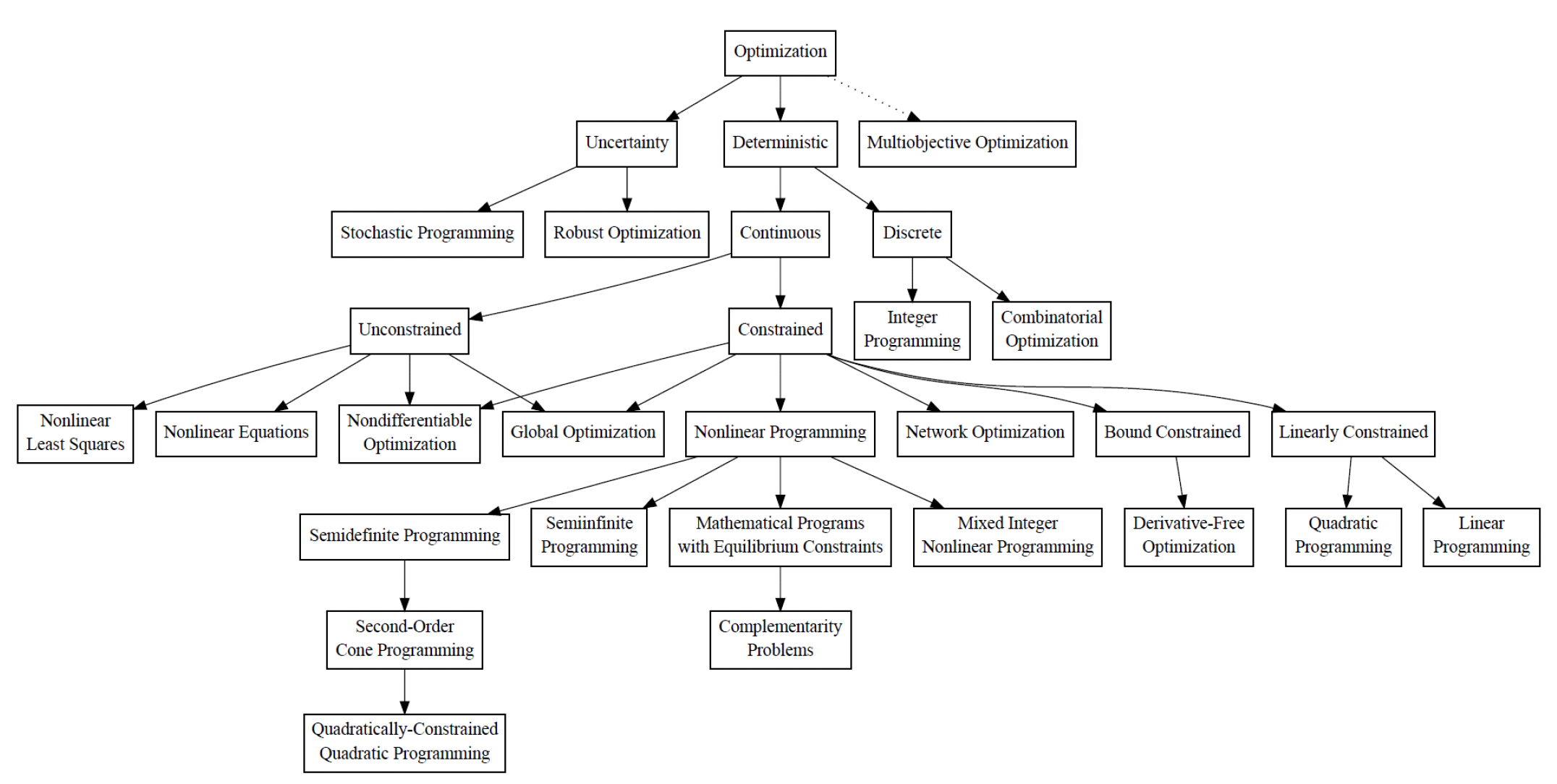
An alternate model, though, could credibly show that Multi-Objective Decision Optimization (MODO) could be positioned at the top of the optimization taxonomy and right above a Single Objective Optimization (SOO) respective box, since SingleObjective optimization can be simply seen as a limited case of Multi-Objective, with all the other branches below relevant to both of them.
In Multi-Criteria Decision Optimization, we need to formulate problems with more than one objective, since a single objective with several constraints may not adequately represent the problems faced and there is a vector of objectives that must be traded off in some way:

F(x) = [F1(x), F2(x),...,Fm(x)]

The relative importance of these objectives is not generally known until the system’s best capabilities are determined, and trade-offs between the objectives fully understood. As the number of objectives increases, trade-offs are likely to become complex and less easily quantified. The decision maker must rely on his or her intuition and ability to express preferences throughout the optimization cycle. Thus, requirements for a multi-objective design strategy must enable a natural problem formulation to be expressed and be able to solve the problem and enter preferences into a numerically tractable and realistic design problem.

So, Multi-objective decision optimization involves minimizing or maximizing multiple objective functions (or else a vector of objectives F(x)) that that can be subject to several constraints or bounds:

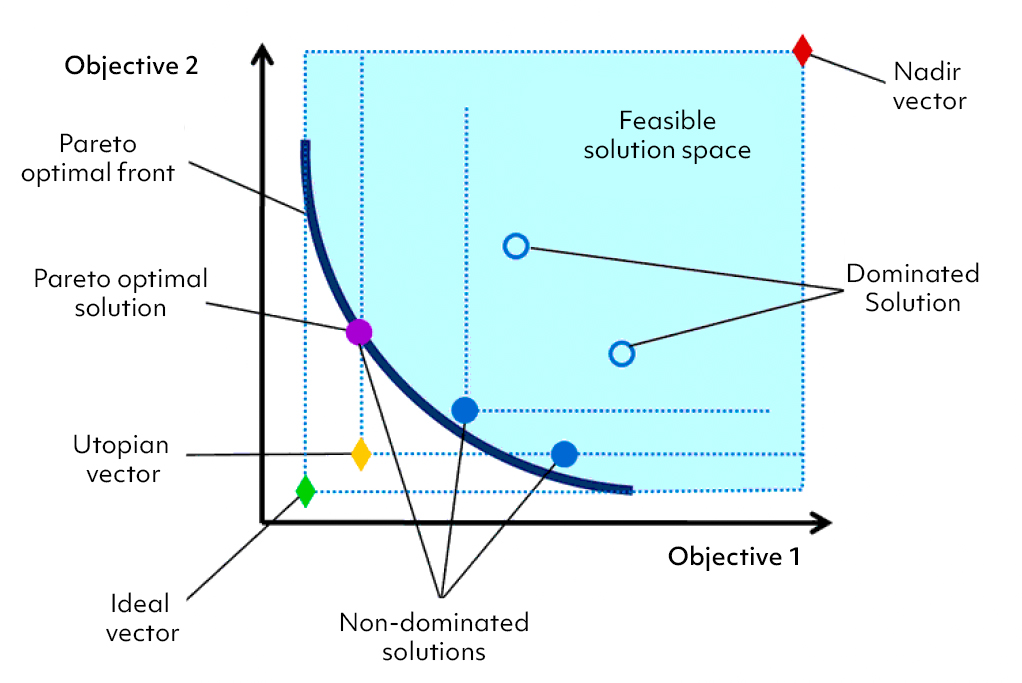
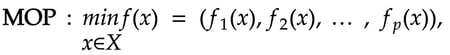Because F(x) is a vector, if any of the components of F(x) are competing, there is no unique solution to this problem. Instead, the concept of noninferiority  (also called Pareto optimality), must be used to characterize the objectives. A Pareto optimal solution refers to a set of solutions, around which there is no way of improving any objective without degrading at least one other objective or else an improvement in one objective requires a degradation of another (a non-inferior set of solutions). The set of Pareto optimal outcomes is often called the Pareto front, Pareto frontier, or Pareto boundary.

Figure 3

The Bi-objective Pareto frontier example6 shows the set of Pareto optimal solutions (those that are not dominated by any other feasible solutions) for a problem. The shaded area represents the area of potentially feasible solutions,’ and those pareto optimal front solutions that are closer (with the lower Euclidean distance) to the ideal vector point are the preferred multi-objective solutions. The same Minimum Euclidean distance measure applies to optimum solutions in the tri-objective7 or any other multi-objective case.

Some example problems include analyzing design tradeoffs, selecting an optimal product or process design, or any other application where you need an optimal solution with tradeoffs between two or more conflicting objectives.

Lexicographic (Sequential) vs. Blended Multi-Objective Optimization

Optimization problems with multiple linear objective functions can be solved by employing modern commercial solvers (e.g., Gurobi or CPLEX in PLEXOS) that offer a mixture of blended and lexicographic or hierarchical optimization.

A lexicographic objective supposes that a priority order has been given among the various objective functions. This order allows you to define a lexicographic order among solutions. A solution is lexicographically smaller than another if it is smaller in the first objective where they differ (following the order). An optimal solution is then lexicographically minimal (or maximal, depending on the optimization sense⁸).

A blended objective is simply the linear combination of several goals with given weights. PLEXOS with Gurobi & CPLEX solvers can combine and handle blended and lexicographic objectives in the same optimization problem. Both weight and priority are always specified for each objective, seamlessly integrating the blended and hierarchical approaches.

More detail on how hierarchical objectives are handled is needed to understand how this works. The solver performs separate optimization steps when someone specifies a different priority for each objective. In each step, in decreasing priority order, it optimizes for the current objective, multiplied by its Objective Weight attribute, while imposing constraints ensuring that the quality of higher-priority objectives isn’t degraded by more than some specified tolerances (either Absolute Tolerance or a Relative (%) Tolerance value).

PLEXOS Case Study: Multi-Objective Decision Optimization in PLEXOS Power Generation Unit Commitment and Dispatch Modelling

PLEXOS has been demonstrated as a real-time dispatch or ex-ante or ex-post market-clearing engine e.g., to audit the operation of other market-clearing engines and simulation software. Now PLEXOS has demonstrated the ability to do Multi-Objective Decision Optimization.

A multi objective function allows the user to specify additional objectives, beyond the usual profit maximization or cost minimization in the classical Unit Commitment/ Energy Dispatch (UC/ED) problem. The newly developed PLEXOS multi-objective optimization capability was employed and demonstrated in a Great Britain and surrounding countries PLEXOS study model, in a variety of UC/ED cases that multi-objective decision optimization can be applied, bringing significant added value to PLEXOS users globally. The extent and variety of cases in the UC/ ED field of applications is already enormous.

Firstly, the single objective of maximizing the profits of a company’s generation assets portfolio was demonstrated along with the company’s unit commitment and the respective energy dispatch of its generators. This is usually set up in PLEXOS as a Price (input) Based Unit Commitment and Dispatch plan problem, with forward electricity market price curves as an input. This then compared against several respective multi-objective UC/ED plan scenarios.

A first test was conducted against historical (known) price outcomes to try to re-optimize the unit commitment and dispatch plan of a generation company with a substantial portfolio of coal and other thermal generation assets (OCGTs, CCGTs & other). Its significant emissions costs were considered in order to maximize its net portfolio profits, in a PLEXOS demo GB2016 electricity market model. The model compared typical single (max profit) objective models’ resulted generators’ dispatching plans against various multi-respective objective models’ solutions plans, that have revealed the strength and enormous value of the later, obtaining also several associated Pareto frontiers.

FIGURE 4: PLEXOS GB MARKET CASE STUDY MODEL OF MULTI-OBJECTIVE OPTIMIZATION

In this example, specifying a secondary objective of minimizing the total system’s costs in addition to a third objective of minimizing the company’s total generated emissions, a 3D Pareto frontier was obtained which has been projected and shown in the 2D figure below.

FIGURE 5: 3D MULTI-OBJECTIVE OPTIMIZATION PARETO FRONTIER OF GB GENERATION COMPANY PORTFOLIO, “HEAVY” ON THERMAL GENERATION ASSETS.

Note that the bubbles’ size and filled or empty bubbles representing respective higher/lower generation portfolio profits or losses. Remarkably, even for such a coal heavy generation portfolio, there are still several profitable Pareto frontier points as seen in the higher left corner of the graph. While emissions are higher, total system costs are lower. Additionally, the low right corner of the graph shows where emissions production is lower and total system costs are not significantly higher.

Figure 6 shows another case, with the resulted unit commitment and dispatch plan of the above company’s generation portfolio. All company’s plants dispatching (total generation stuck) are shown for 1 week. The multi- objective (max profit/min system cost) detail per plant dispatching results are compared to the resulted total dispatch of the same power plants by a single-objective (max profit) run, the later shown with the red line.

FIGURE 6: MULTI-OBJECTIVE V SINGLE-OBJECTIVE OPTIMUM DISPATCH PLAN OF COMPANY’S GENERATION PORTFOLIO

In figure 7 the orange line represents the Company’ portfolio (Generation) Net profits results from the above multi-objective decision optimisation of dispatching plan, while the blue line those profits that would have been resulted from the respective single profit maximisation objective dispatching plan.

FIGURE 7 MULTI-OBJECTIVE V SINGLE-OBJECTIVE NET PROFITS OF COMPANY’S GENERATION PORTFOLIO

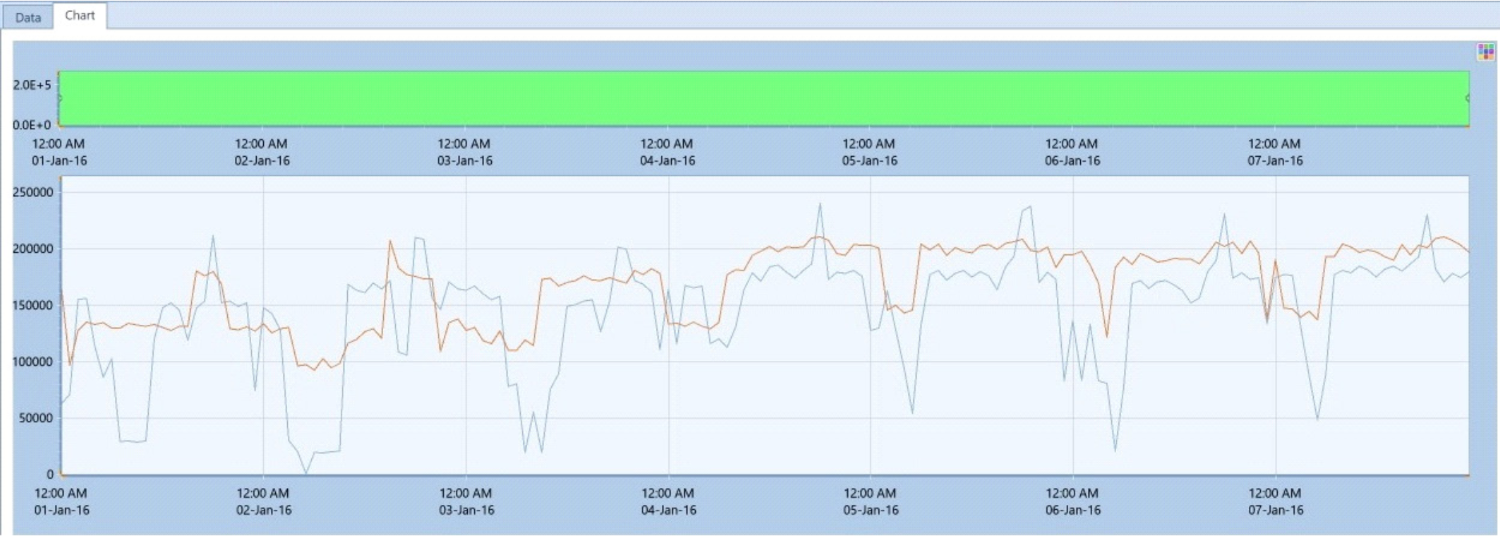
In both figures 6 & 7 it is clearly shown that both the resulted Company’s total generation/energy dispatching as well as, its net profits were much higher in the multi-objective optimisation case.

In another example, we specify a secondary objective of minimizing company’s generators ramping, examining all similar economically optimal solutions, and chose the solution which minimized the ramping of units, essentially smoothing out the dispatch profile to something which can be used operationally. The following two (2) graphs show two output schedules for two units of the portfolio.

FIGURE 8: MULTI-OBJECTIVE V SINGLE-OBJECTIVE OPTIMUM DISPATCH PLAN OF TWO COMPANY’S GENERATORs

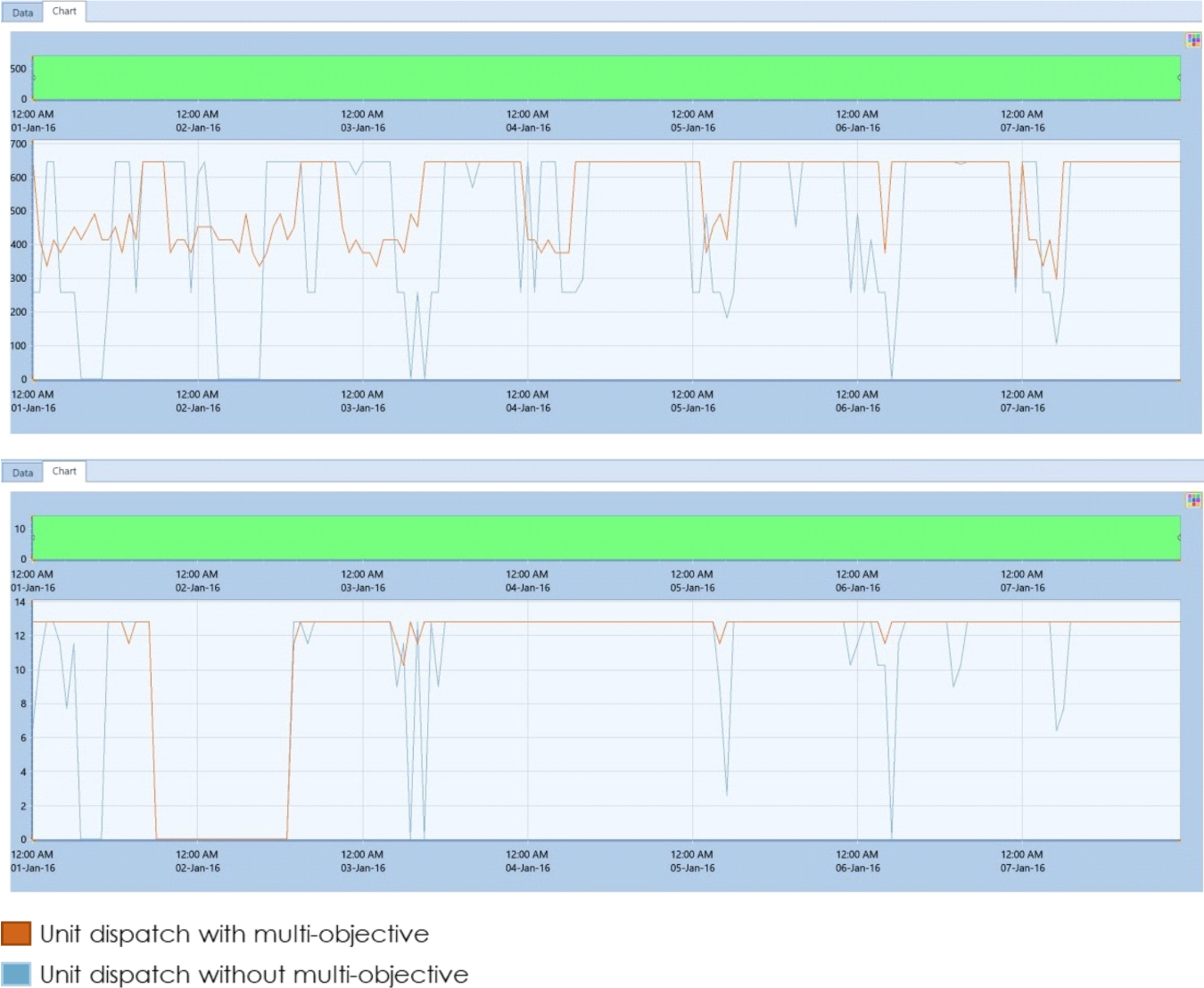
Both single and multi-objective outputs are from the same model/problem and resulted in the same total revenue however, the spikey nature of the dispatch of the plants was smoothed out over all units in the portfolio’s multi-objective decision optimization case.

Conclusion

In the Era of Complexity and Big Data, Energy Companies try to harness analytics technologies to predict trends and prescribe the proper course of action to achieve their core objectives. Information (data) just for information, or else information that cannot be transformed into valuable knowledge and subsequent actions, it is merely useless.

Predictive analytics answers what may happen, while prescriptive analytics and in particular, Multi-Objective Decision Optimization is the only method available that can lead to specific actions, providing feasible and optimum answers to multiple what-if scenarios and taking into account various objectives’ trade-offs and potential futures. PLEXOS successfully provides for many years now Predictive Analytics (Scenario Analysis, MC Simulations and Stochastic Optimization) capacity where in combination with the new Multi-Objective Decision Optimization functionality can yield maximum benefits at the enterprise level.

“Next analytics revolution is the ability to couple predictive technologies with prescriptive technologies...”

Grant Thornton